Location Analysis: Single Array Error Model

The quantitative amplification of small amounts of DNA generates some uncertainty in values for the low intensity spots. In order to track that uncertainty and average repeated experiments with appropriate related weights, we adopted a single-array error model first described by Hughes et al. (2000).

According to this error model, the significance of a measured ratio at a spot is defined by a statistic X, which takes the form

(1)

where a_1,2 are the intensities measured in the two channels for each spot, _1,2 are the uncertainties due to background subtraction, and f is a fractional multiplicative error such as would come from hybridization non-uniformities, fluctuations in the dye incorporation efficiency, scanner gain fluctuations, etc. The distribution of X across all spots on a chip is approximately normal. The parameters  and f were chosen based on control hybridizations such that X had unit variance. The significance of a change of magnitude x is then calculated as

(2)	p = 1-Erf(X)

For each factor, three independent experiments were performed and each of the three samples were analyzed individually using the single-array error model described above. The average binding ratio and associated p-value from the triplicate experiments were then calculated using a weighted average analysis method adapted from Hughes et al. (2000).

Briefly, the binding ratio is expressed as the log₁₀(a₂/a₁), where a₁,a₂ are the intensities measured in the two channels for each spot. The uncertainty in the log(Ratio) is defined as

(3)

where X is the statistic derived from the single array error model. We use the minimum-variance weighted average to compute the mean log₁₀(a₂/a₁) of each spot:

(4)

(5)

Here _i is the error of log₁₀(a₂/a₁) from (3), x_i stands for i-th measurement of log₁₀(a₂/a₁), n is the number of repeats.

The error of 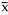 can be computed in two ways. One is to propagate the errors _i , another is from the scatter of x_i:

(6)

For the average of multiple slides, the significance statistic X is computed as:

(7)

and the confidence is computed using Equation (2) from the single array error model.